Lực hướng tâm là gì? Công thức lực hướng tâm

02/08/23

Chuyên mục: Kiến Thức Chung

Thực tế, lực hướng tâm được ứng dụng và giải thích nhiều ở nhiều hiện tượng vật lý trong thực tế. Vậy lực hướng tâm được định nghĩa như thế nào?

Lực hướng tâm là gì? Công thức lực hướng tâm [Kiến thức 2023]

Lực Hướng Tâm Là Gì? Tổng Hợp Kiến Thức Từ A-Z & Bài Tập Vận Dụng

Trong thực tế cuộc sống và kỹ thuật, lực hướng tâm được ứng dụng và giải thích cho rất nhiều hiện tượng vật lý thú vị, từ vệ tinh bay quanh Trái Đất đến chiếc xe ôm cua trên đường. Vậy lực hướng tâm được định nghĩa như thế nào? Công thức tính lực hướng tâm ra sao? Hãy cùng Mecsu tìm hiểu chi tiết thông qua bài viết dưới đây nhé.

Lực hướng tâm là gì?

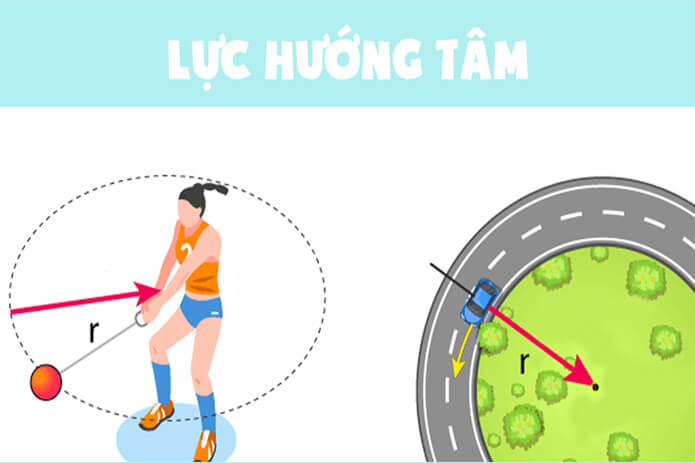
Lực hướng tâm (Centripetal force) là một lực (hoặc hợp lực của các lực) tác dụng lên một vật đang chuyển động tròn đều, có phương trùng với bán kính quỹ đạo và chiều luôn hướng vào tâm quay. Lực này giữ cho vật không bị văng ra khỏi quỹ đạo và gây ra cho vật một gia tốc hướng tâm.

Hình ảnh minh họa khái niệm lực hướng tâm

→ Đơn vị của lực hướng tâm

Cũng giống như các loại lực khác trong hệ đo lường quốc tế (SI), đơn vị của lực hướng tâm là Newton (N).

→ Đặc điểm quan trọng của lực hướng tâm

Cần lưu ý rằng, bản chất thật sự của lực hướng tâm không phải là một loại lực mới (như lực hấp dẫn, lực đàn hồi hay lực ma sát). Nó chỉ là tên gọi cho vai trò của một lực (hoặc hợp lực) nào đó khi nó có tác dụng giữ cho vật chuyển động tròn.

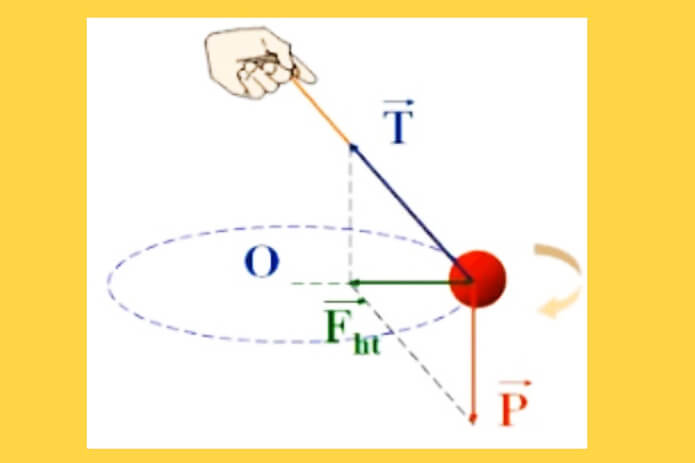
Đặc điểm vecto lực hướng tâm hướng vào tâm O

Điểm đặt: Tại vật chuyển động.
Phương: Trùng với bán kính quỹ đạo.
Chiều: Luôn hướng vào tâm quay (tâm quỹ đạo).
Vai trò: Gây ra gia tốc hướng tâm (a_ht) cho vật.

Ví dụ minh họa: Khi quay một hòn đá buộc vào sợi dây, hợp lực của lực căng dây và trọng lực (ở vị trí thấp nhất) đóng vai trò là lực hướng tâm. Lực này có chiều hướng vào tâm quay O.

→ Ví dụ thực tế về lực hướng tâm

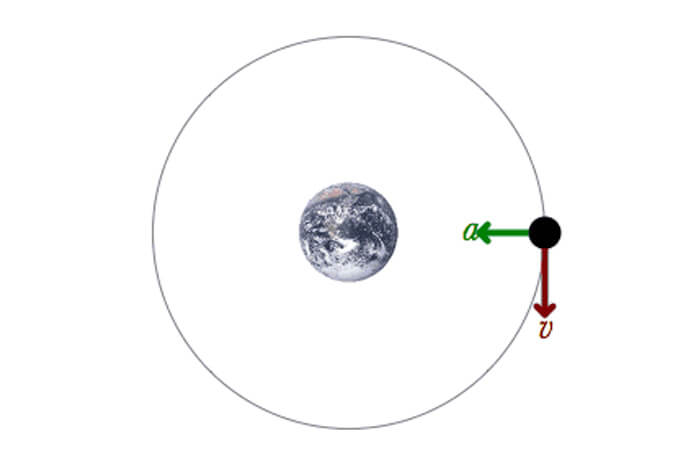
Vệ tinh nhân tạo: Lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm, giữ cho vệ tinh chuyển động tròn quanh Trái Đất.
Vật trên bàn xoay: Khi đặt một vật trên bàn quay, lực ma sát nghỉ đóng vai trò là lực hướng tâm giữ cho vật không bị trượt ra ngoài.
Xe vào cua: Khi xe đi vào khúc cua, lực ma sát nghỉ giữa bánh xe và mặt đường (ngang) đóng vai trò lực hướng tâm.
Đường nghiêng (Banking road): Đường cao tốc và đường sắt ở các khúc cua thường được làm nghiêng về phía tâm. Lúc này, hợp lực của trọng lực (P) và phản lực (N) của mặt đường sẽ tạo thành lực hướng tâm, giúp xe và tàu hỏa di chuyển an toàn ở tốc độ cao mà không cần dựa hoàn toàn vào ma sát.

Ví dụ về lực hướng tâm trong chuyển động tròn

Công thức tính lực hướng tâm

Theo định luật II Newton, lực hướng tâm được tính bằng tích của khối lượng và gia tốc hướng tâm:

F_ht = m × a_ht = m × (v² / r) = m × ω² × r

Trong đó:

F_ht: Lực hướng tâm (N).
m: Khối lượng của vật (kg).
a_ht: Gia tốc hướng tâm (m/s²).
v: Tốc độ dài của vật chuyển động tròn đều (m/s).
r: Bán kính quỹ đạo tròn (m).
ω (omega): Tốc độ góc của vật chuyển động tròn đều (rad/s).

Bài tập lực hướng tâm có lời giải chi tiết

Bài tập vận dụng lực hướng tâm

Dạng 1: Tính lực hướng tâm và các đại lượng liên quan

Kiến thức cần nhớ:

Chu kỳ: T = 2π / ω (s)
Tần số: f = 1 / T = ω / 2π (Hz)
Tốc độ góc: ω = v / r = 2π / T = 2πf (rad/s)
Gia tốc hướng tâm: a_ht = v² / r = rω²
Mối liên hệ tốc độ dài và góc: v = rω

Ví dụ 1: Xe đạp của một vận động viên đang chuyển động thẳng đều với vận tốc v = 36 km/h. Giả sử bán kính của lốp xe là 40 cm. Tính tốc độ góc và gia tốc hướng tâm tại một điểm trên lốp xe.

Giải:

Đổi đơn vị: v = 36 km/h = 10 m/s; r = 40 cm = 0.4 m.
Tốc độ góc: ω = v / r = 10 / 0.4 = 25 rad/s.
Gia tốc hướng tâm tại điểm trên lốp: a_ht = v² / r = 10² / 0.4 = 250 m/s².

Dạng 2: Tính áp lực của vật tại điểm cao nhất của vòng cầu

Phương pháp:

Vẽ hình, phân tích lực tác dụng lên vật (Trọng lực P, Phản lực N).
Xác định chiều dương hướng vào tâm quay.
Viết phương trình định luật II Newton theo phương hướng tâm: ∑F = m.a_ht.

Công thức cụ thể:

Cầu vồng lên (Cầu lồi): Tại điểm cao nhất, P cùng chiều a_ht, N ngược chiều.
Ta có: P - N = m.a_ht ⇒ N = P - m.a_ht = mg - m(v²/r).
(Lực nén lên cầu nhỏ hơn trọng lượng P).
Cầu vồng xuống (Cầu lõm): Tại điểm thấp nhất, N cùng chiều a_ht, P ngược chiều.
Ta có: N - P = m.a_ht ⇒ N = P + m.a_ht = mg + m(v²/r).
(Lực nén lên cầu lớn hơn trọng lượng P).

Ví dụ 2: Một ô tô khối lượng 2,5 tấn chạy qua cầu vượt (dạng cầu lồi) với vận tốc không đổi 54 km/h. Cầu vượt là cung tròn bán kính 100m. Tính áp lực của ô tô lên cầu tại điểm cao nhất. Lấy g = 9,8 m/s².

Giải:

Đổi đơn vị: m = 2500 kg; v = 54 km/h = 15 m/s; r = 100 m.
Tại điểm cao nhất, các lực tác dụng lên xe gồm Trọng lực P (hướng xuống) và Phản lực N (hướng lên). Hợp lực của chúng tạọ ra gia tốc hướng tâm (hướng xuống).
Theo định luật II Newton (chiều dương hướng tâm): P - N = m(v²/r)
Suy ra áp lực N: N = P - m(v²/r) = m(g - v²/r)
Thay số: N = 2500 * (9.8 - 15²/100) = 2500 * (9.8 - 2.25) = 2500 * 7.55 = 18.875 N.

Mô hình lực tác dụng lên ô tô khi qua cầu cong

Dạng 3: Lực đàn hồi / Lực ma sát đóng vai trò lực hướng tâm

Khi vật gắn vào lò xo và quay, lực đàn hồi là lực hướng tâm: F_đh = F_ht.
Khi vật đặt trên bàn quay, lực ma sát nghỉ là lực hướng tâm: F_ms = F_ht.

Bài tập 1: Vật khối lượng 100g gắn vào đầu lò xo có chiều dài tự nhiên l₀ = 20cm, độ cứng k = 20 N/m. Cho hệ quay đều trên mặt phẳng nằm ngang không ma sát với tần số 60 vòng/phút. Tính độ biến dạng của lò xo.

Giải:

m = 0.1 kg; l₀ = 0.2 m; f = 60 vòng/phút = 1 vòng/s = 1 Hz.
Tốc độ góc: ω = 2πf = 2π rad/s.
Khi lò xo dãn ra đoạn Δl, bán kính quỹ đạo là r = l₀ + Δl.
Lực đàn hồi đóng vai trò lực hướng tâm: F_đh = F_ht
k.Δl = m.ω².r = m.ω².(l₀ + Δl)
⇒ k.Δl - m.ω².Δl = m.ω².l₀
⇒ Δl = (m.ω².l₀) / (k - m.ω²)
Thay số: ω² ≈ 40. Δl = (0.1 * 40 * 0.2) / (20 - 0.1 * 40) = 0.8 / 16 = 0.05 m = 5 cm.

Bài tập 2 (Vật trên bàn xoay): Một vật khối lượng m = 20g đặt ở mép bàn xoay hình tròn bán kính r = 1m. Lực ma sát nghỉ cực đại giữa vật và bàn là 0.08N. Tính tần số quay lớn nhất để vật không bị văng ra khỏi bàn.

Giải:

m = 0.02 kg; r = 1 m; F_{ms_max} = 0.08 N.
Để vật không văng ra, lực hướng tâm cần thiết phải nhỏ hơn hoặc bằng lực ma sát nghỉ cực đại mà bàn có thể cung cấp: F_ht ≤ F_{ms_max}
m.ω².r ≤ F_{ms_max}
⇒ ω² ≤ F_{ms_max} / (m.r) = 0.08 / (0.02 * 1) = 4
⇒ ω ≤ 2 rad/s.
Tần số f = ω / 2π ≤ 2 / 2π = 1/π (vòng/s).

MUA NGAY HÀNG CÔNG NGHIỆP GIÁ TỐT TẠI MECSU

Tham khảo thêm tại Mecsu

>>> 800+ Mã Sản Phẩm Long Đền: https://mecsu.vn/san-pham/long-den.WR

>>> 800+ Mã Sản Phẩm Đai Ốc: https://mecsu.vn/san-pham/tan-dai-oc.GB

Mời anh em xem thêm các bài viết vật lý khác:

Lực hướng tâm là khái niệm quan trọng và được ứng dụng rất nhiều trong cuộc sống hàng ngày cũng như kỹ thuật. Hy vọng với những kiến thức lý thuyết và bài tập thực tế mà Mecsu vừa giới thiệu sẽ giúp các bạn hiểu rõ bản chất và áp dụng dễ dàng hơn.